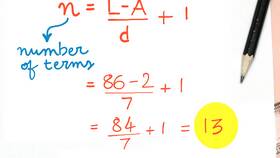Арифметическая прогрессия - это последовательность чисел, в которой каждое последующее число отличается от предыдущего на постоянную величину (разность прогрессии). Рассмотрим методы вычисления суммы членов такой прогрессии.
Содержание
Основные понятия
Характеристики прогрессии
- a₁ - первый член прогрессии
- d - разность прогрессии
- aₙ - n-ный член прогрессии
- n - количество членов
- Sₙ - сумма первых n членов
Формула n-го члена
| Обозначение | Формула |
| n-ный член | aₙ = a₁ + d(n-1) |
Формулы для вычисления суммы
Основная формула
Sₙ = n/2 × (2a₁ + d(n-1))
Альтернативная формула
Sₙ = n/2 × (a₁ + aₙ)
Пошаговый алгоритм вычисления
Когда известны первый член и разность
- Определите количество членов прогрессии (n)
- Подставьте значения в формулу Sₙ = n/2 × (2a₁ + d(n-1))
- Выполните вычисления в скобках
- Умножьте на n/2
Когда известны первый и последний члены
| Шаг | Действие |
| 1 | Определите количество членов (n) |
| 2 | Используйте формулу Sₙ = n/2 × (a₁ + aₙ) |
| 3 | Сложите первый и последний члены |
| 4 | Умножьте на количество членов и разделите на 2 |
Примеры вычислений
Пример 1: Простая прогрессия
- Дано: 2, 5, 8, 11, 14 (n=5, a₁=2, d=3)
- Решение: S₅ = 5/2 × (2×2 + 3(5-1)) = 2.5 × (4 + 12) = 2.5 × 16 = 40
- Проверка: 2 + 5 + 8 + 11 + 14 = 40
Пример 2: Использование альтернативной формулы
| Дано | Решение |
| a₁ = 10, aₙ = 50, n=9 | S₉ = 9/2 × (10 + 50) = 4.5 × 60 = 270 |
Особые случаи
Сумма натуральных чисел
Сумма первых n натуральных чисел: Sₙ = n(n+1)/2
Бесконечная арифметическая прогрессия
- Сумма бесконечной арифметической прогрессии расходится
- При n→∞, Sₙ→±∞ в зависимости от знака d
Практическое применение
В финансовых расчетах
- Расчет суммы регулярных платежей с постоянным изменением
- Определение общей суммы амортизационных отчислений
- Планирование накоплений с постоянным увеличением взносов
В физических задачах
| Область | Применение |
| Механика | Расчет пути при равноускоренном движении |
| Экономика | Моделирование линейного роста показателей |
Формулы суммы арифметической прогрессии позволяют быстро вычислять общее значение последовательности чисел без необходимости сложения каждого члена по отдельности. Понимание этих методов полезно как в учебных задачах, так и в практических расчетах.