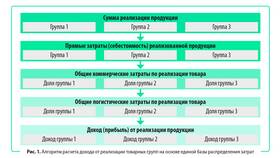
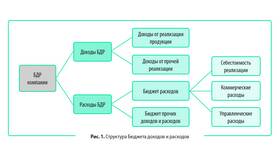
Сумма представляет собой результат сложения двух или более чисел, величин или математических выражений. В различных областях математики, финансов и естественных наук расчет суммы может иметь свои особенности.
Содержание
Основные виды сумм
| Тип суммы | Определение |
| Арифметическая сумма | Результат сложения чисел |
| Алгебраическая сумма | Сложение с учетом знаков чисел |
| Геометрическая сумма | Сложение векторов или отрезков |
Формулы для расчета сумм
- Простая сумма: S = a + b + c
- Сумма арифметической прогрессии: Sₙ = n/2 × (2a₁ + (n-1)d)
- Сумма геометрической прогрессии: Sₙ = a₁(1 - qⁿ)/(1 - q)
- Сумма ряда: S = Σ(aₙ) от n=1 до ∞
Примеры расчетов сумм
Пример 1: Простая сумма
Даны числа: 5, 12, 8, 3
Сумма равна: 5 + 12 + 8 + 3 = 28
Пример 2: Сумма арифметической прогрессии
Первый член a₁ = 3, разность d = 4, количество членов n = 5
Сумма равна: 5/2 × (2×3 + (5-1)×4) = 2.5 × (6 + 16) = 2.5 × 22 = 55
Свойства суммы
| Свойство | Формулировка |
| Коммутативность | a + b = b + a |
| Ассоциативность | (a + b) + c = a + (b + c) |
| Дистрибутивность | a × (b + c) = a × b + a × c |
Применение сумм в различных областях
- Финансы: расчет общей суммы доходов или расходов
- Физика: сложение векторов сил
- Статистика: вычисление суммарных показателей
- Программирование: агрегация данных
Особые случаи суммирования
- Бесконечные ряды
- Условно сходящиеся ряды
- Суммы с комплексными числами
- Векторные суммы
Правильное понимание и расчет суммы является фундаментальным навыком в математике и ее приложениях. В зависимости от конкретной задачи, методы вычисления суммы могут значительно отличаться.